LANGSUNG SAJA KLIK LINK BERIKUT!!!! >>> https://helmifadhiel.wordpress.com/2015/11/16/karnaugh-map-beserta-penjelasannya/
Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dari rangkaian logika yang sedang kita hitung.
| Rumus untuk menentukan jumlah kotak pada K-Map adalah 2^n yang manan adalah banyaknya variabel / inputan. |
Langkah – langkah pemetaan K-Map secara umum :
- Menyusun aljabar Boolean terlebih dahulu
- Menggambar rangkaian digital
- Membuat Table Kebenarannya
- Merumuskan Tabel Kebenarannya
- Lalu memasukkan rumus Tabel Kebenaran ke K-Map (Kotak-kotak)
Penyederhanaan Dua Variabel
Catatan : Bar = ‘
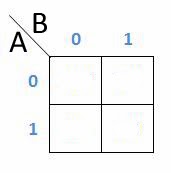
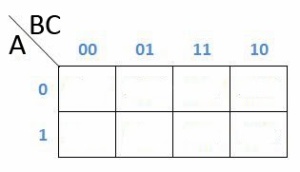
Tabel dari K-Map 2 variabel adalah seperti dibawah ini
Contoh Soal :
H = AB + A’B+AB’
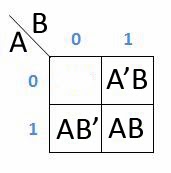
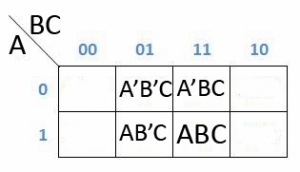
Maka cara pengerjaanya seperti dibawah ini
Bar (‘) atau aksen biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar aksen.
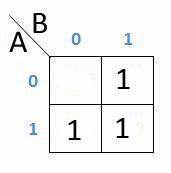
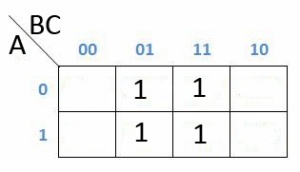
Dan dapat dipermudah lagi menjadi dibawah ini :
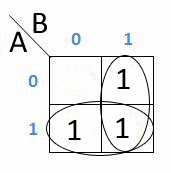
Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya:
Karena kolom ber angka 1 dan baris ber angka 1 memenuhi setiap garisnya, maka dapat disimpulkan kalau H = AB + A’B+AB’ K-Map nya adalah AB/BA
Penyederhanaan Tiga Variabel
Catatan : Bar = ‘
Tabel dari K-Map 3 variabel adalah seperti dibawah ini
Contoh Soal
H = ABC + A’BC+A’B’C+AB’C
Maka cara pengerjaanya seperti dibawah ini
Dan dapat dipermudah lagi menjadi dibawah ini
Sekarang kita lihat, karena yang memenuhi setiap kotaknya adalah baris 01 dan 11 sedangkan simbol 01 artinya adalah (B’C) dan 11 artinya adalah (BC) dan simbol yang tidak ada aksen nya hanya C, maka H = ABC + A’BC+A’B’C+AB’C adalah C.
Penyederhanaan 4 variabel
Catatan : Bar = ‘
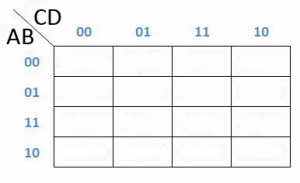
Tabel dari K-Map 4 variabel adalah seperti dibawah ini :
Contoh Soal
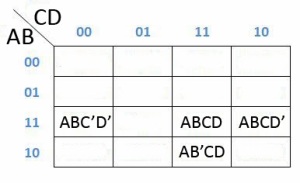
H = ABCD + ABCD’+AB’CD+ABC’D’
Maka cara pengerjaanya seperti dibawah ini
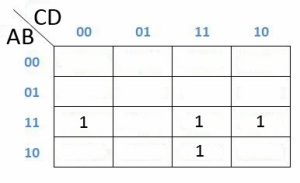
Dan dapat dipermudah lagi menjadi dibawah ini :
Karena yang ada angka 1 nya ada di kolom dan baris 1100, 1111, 1110 dan 1011, yaitu AB, ABCD, ABC dan ACD maka jika kita eliminasi dengan cara mengambil huruf yang sama saja menjadi AB + ABC + ACD.
DISALIN DARI :
https://helmifadhiel.wordpress.com/2015/11/16/karnaugh-map-beserta-penjelasannya/